Find a Family of Solutions to the Differential Equation (X2ã¢ë†â€™xy)dx+xdy=0

Solve Differential Equations with ODEINT

Differential equations are solved in Python with the Scipy.integrate package using function odeint or solve_ivp.

ODEINT requires iii inputs:

            y = odeint(model, y0, t)          

1. model: Function proper noun that returns derivative values at requested y and t values as dydt = model(y,t)
2. y0: Initial conditions of the differential states
3. t: Time points at which the solution should be reported. Additional internal points are often calculated to maintain accuracy of the solution but are not reported.

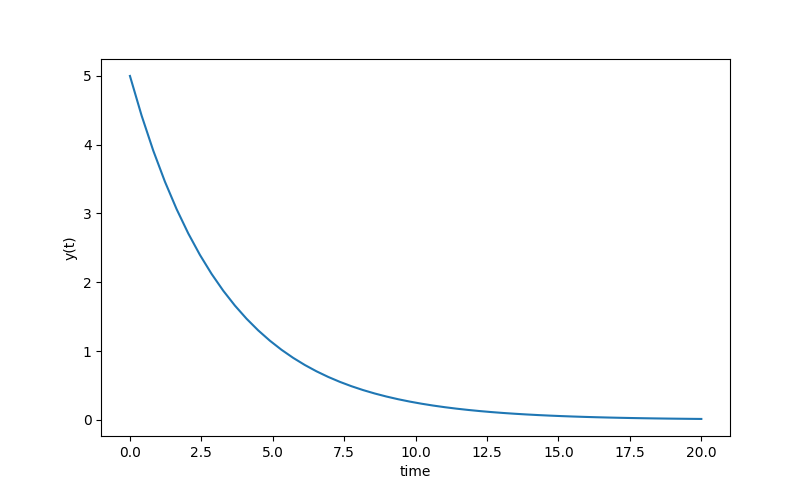
An case of using ODEINT is with the following differential equation with parameter k=0.three, the initial condition y₀=v and the post-obit differential equation.

$$\frac{dy(t)}{dt} = -k \; y(t)$$

The Python lawmaking first imports the needed Numpy, Scipy, and Matplotlib packages. The model, initial conditions, and time points are defined every bit inputs to ODEINT to numerically calculate y(t).

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot every bit plt

# function that returns dy/dt
def model(y,t):
m = 0.3
dydt = -m * y
return dydt

# initial condition
y0 = 5

# fourth dimension points
t = np.linspace ( 0 , 20 )

# solve ODE
y = odeint(model,y0,t)

# plot results
plt.plot (t,y)
plt.xlabel ( 'time' )
plt.ylabel ( 'y(t)' )
plt.prove ( )

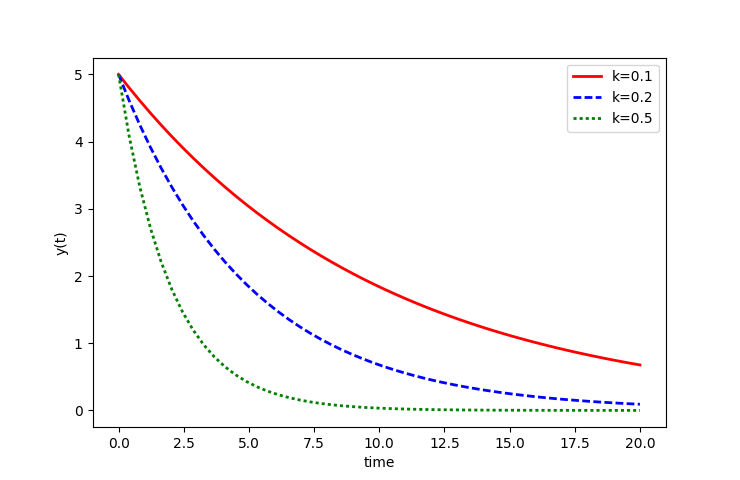
An optional fourth input is args that allows additional information to be passed into the model role. The args input is a tuple sequence of values. The argument chiliad is now an input to the model role past including an addition argument.

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot every bit plt

# role that returns dy/dt
def model(y,t,k):
dydt = -1000 * y
return dydt

# initial condition
y0 = 5

# time points
t = np.linspace ( 0 , 20 )

# solve ODEs
k = 0.1
y1 = odeint(model,y0,t,args= (m, ) )
k = 0.two
y2 = odeint(model,y0,t,args= (k, ) )
k = 0.five
y3 = odeint(model,y0,t,args= (k, ) )

# plot results
plt.plot (t,y1, 'r-' ,linewidth= 2 ,characterization= 'grand=0.ane' )
plt.plot (t,y2, 'b--' ,linewidth= two ,label= 'k=0.two' )
plt.plot (t,y3, 'g:' ,linewidth= ii ,label= 'k=0.5' )
plt.xlabel ( 'time' )
plt.ylabel ( 'y(t)' )
plt.legend ( )
plt.evidence ( )

Exercises

Find a numerical solution to the following differential equations with the associated initial conditions. Expand the requested time horizon until the solution reaches a steady country. Evidence a plot of the states (10(t) and/or y(t)). Report the final value of each state every bit `t \to \infty`.

---

Problem ane

$$\frac{dy(t)}{dt} = -y(t) + 1$$

$$y(0) = 0$$

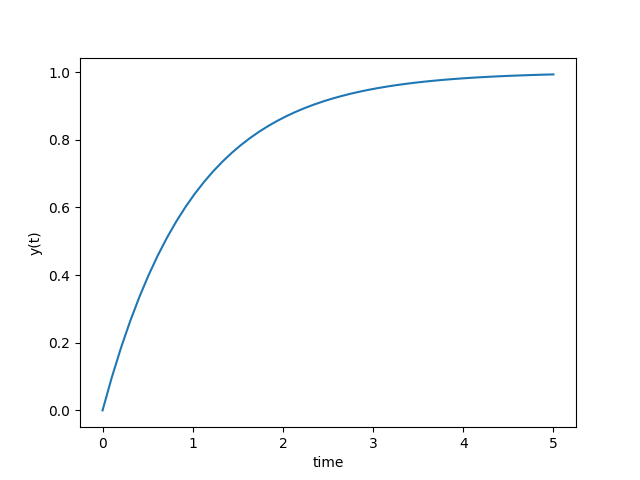
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dy/dt
def model(y,t):
dydt = -y + 1.0
return dydt

# initial condition
y0 = 0

# time points
t = np.linspace ( 0 , 5 )

# solve ODE
y = odeint(model,y0,t)

# plot results
plt.plot (t,y)
plt.xlabel ( 'time' )
plt.ylabel ( 'y(t)' )
plt.bear witness ( )

---

Problem ii

$$v \; \frac{dy(t)}{dt} = -y(t) + u(t)$$

$$y(0) = one$$

`u` steps from 0 to ii at `t=10`

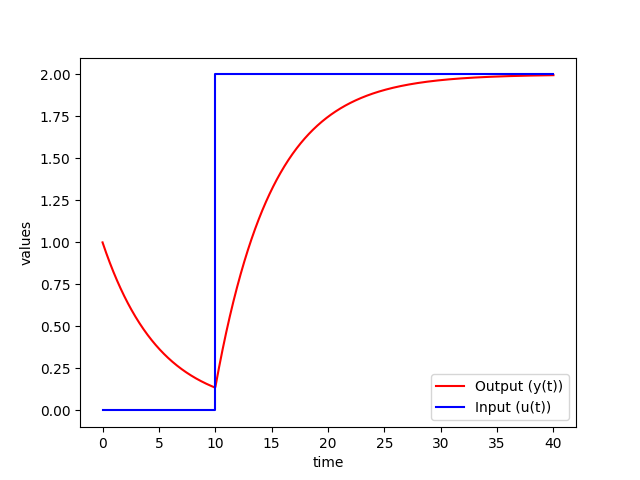
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# part that returns dy/dt
def model(y,t):
# u steps from 0 to 2 at t=10
if t< 10.0:
u = 0
else:
u = 2
dydt = (-y + u)/5.0
return dydt

# initial condition
y0 = 1

# time points
t = np.linspace ( 0 , 40 , g )

# solve ODE
y = odeint(model,y0,t)

# plot results
plt.plot (t,y, 'r-' ,characterization= 'Output (y(t))' )
plt.plot ( [ 0 , 10 , 10 , 40 ] , [ 0 , 0 , 2 , 2 ] , 'b-' ,characterization= 'Input (u(t))' )
plt.ylabel ( 'values' )
plt.xlabel ( 'time' )
plt.legend (loc= 'best' )
plt.show ( )

---

Problem three

Solve for `ten(t)` and `y(t)` and bear witness that the solutions are equivalent.

$$\frac{dx(t)}{dt} = iii \; exp(-t)$$ $$\frac{dy(t)}{dt} = 3 - y(t)$$ $$ten(0) = 0$$ $$y(0) = 0$$

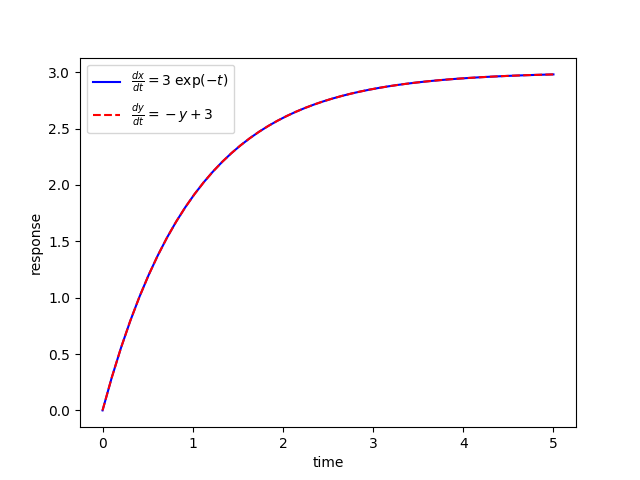
import numpy every bit np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# part that returns dz/dt
def model(z,t):
dxdt = 3.0 * np.exp (-t)
dydt = -z[ 1 ] + 3
dzdt = [dxdt,dydt]
render dzdt

# initial status
z0 = [ 0 , 0 ]

# time points
t = np.linspace ( 0 , 5 )

# solve ODE
z = odeint(model,z0,t)

# plot results
plt.plot (t,z[:, 0 ] , 'b-' ,label=r'$\frac{dx}{dt}=3 \; \eastxp(-t)$' )
plt.plot (t,z[:, 1 ] , 'r--' ,label=r'$\frac{dy}{dt}=-y+3$' )
plt.ylabel ( 'response' )
plt.xlabel ( 'time' )
plt.legend (loc= 'best' )
plt.testify ( )

---

Problem iv

$$2 \; \frac{dx(t)}{dt} = -x(t) + u(t)$$

$$5 \; \frac{dy(t)}{dt} = -y(t) + x(t)$$

$$u = 2 \, Southward(t-5), \; x(0) = 0, \; y(0) = 0$$

where `Southward(t-five)` is a stride function that changes from zip to 1 at `t=5`. When information technology is multiplied by two, it changes from zippo to two at that same fourth dimension, `t=5`.

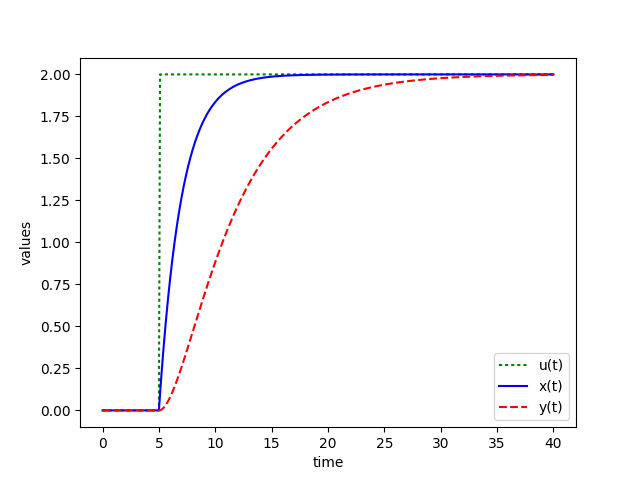
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# role that returns dz/dt
def model(z,t,u):
x = z[ 0 ]
y = z[ 1 ]
dxdt = (-x + u)/two.0
dydt = (-y + ten)/five.0
dzdt = [dxdt,dydt]
return dzdt

# initial status
z0 = [ 0 , 0 ]

# number of time points
n = 401

# time points
t = np.linspace ( 0 , xl ,n)

# stride input
u = np.zeros (northward)
# change to ii.0 at fourth dimension = 5.0
u[ 51:] = 2.0

# shop solution
ten = np.empty_like (t)
y = np.empty_like (t)
# record initial conditions
x[ 0 ] = z0[ 0 ]
y[ 0 ] = z0[ 1 ]

# solve ODE
for i in range ( i ,due north):
# span for next time footstep
tspan = [t[i-1 ] ,t[i] ]
# solve for side by side pace
z = odeint(model,z0,tspan,args= (u[i] , ) )
# store solution for plotting
x[i] = z[ one ] [ 0 ]
y[i] = z[ one ] [ 1 ]
# next initial status
z0 = z[ one ]

# plot results
plt.plot (t,u, 'thousand:' ,label= 'u(t)' )
plt.plot (t,x, 'b-' ,label= 'ten(t)' )
plt.plot (t,y, 'r--' ,label= 'y(t)' )
plt.ylabel ( 'values' )
plt.xlabel ( 'fourth dimension' )
plt.legend (loc= 'best' )
plt.prove ( )

---

---

Some other Python package that solves differential equations is GEKKO. See this link for the same tutorial in GEKKO versus ODEINT.

colliermagesentrage1994.blogspot.com

Source: https://apmonitor.com/pdc/index.php/Main/SolveDifferentialEquations

Share this post