How to Draw Phase Plane Trajectory
Phase Portraits of Linear Systems
Consider a In this section we study the qualitative features of the phase portraits, obtaining a classification of the different possibilities that can ascend. One reason that this is important is considering, equally we will see shortly, information technology will be very useful in the written report of nonlinear systems. The classification will non be quite consummate, because we'll leave out the cases where 0 is an eigenvalue of ![]() .
.
The first step in the nomenclature is to find the characteristic polynomial, ![]() , which will exist a quadratic: nosotros write it as
, which will exist a quadratic: nosotros write it as ![]() where
where ![]() and
and ![]() are real numbers (assuming every bit usual that our matrix
are real numbers (assuming every bit usual that our matrix ![]() has existent entries). The classification will depend mainly on
has existent entries). The classification will depend mainly on ![]() and
and ![]() , and nosotros make a chart of the possibilities in the
, and nosotros make a chart of the possibilities in the ![]() plane.
plane.
Now nosotros look at the discriminant of this quadratic, ![]() . The sign of this determines what blazon of eigenvalues our matrix has:
. The sign of this determines what blazon of eigenvalues our matrix has:
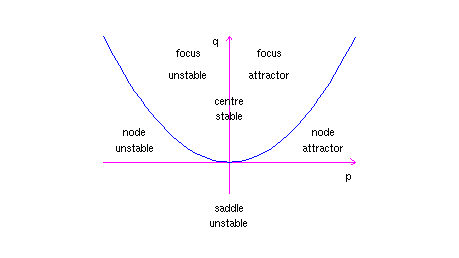
Each of these cases has subcases, depending on the signs (or in the complex case, the sign of the real role) of the eigenvalues. Notation that ![]() is the production of the eigenvalues (since
is the production of the eigenvalues (since ![]() ), so for
), so for ![]() the sign of
the sign of ![]() determines whether the eigenvalues take the aforementioned sign or opposite sign. We will ignore the possibility of
determines whether the eigenvalues take the aforementioned sign or opposite sign. We will ignore the possibility of ![]() , as that would mean 0 is an eigenvalue.
, as that would mean 0 is an eigenvalue.
The sum of the eigenvalues is ![]() , then if they take the same sign this is reverse to the sign of
, then if they take the same sign this is reverse to the sign of ![]() . If the eigenvalues are circuitous, their real role is
. If the eigenvalues are circuitous, their real role is ![]() .
.
Some other important tool for sketching the phase portrait is the post-obit: an eigenvector ![]() for a real eigenvalue
for a real eigenvalue ![]() corresponds to a solution
corresponds to a solution ![]() that is e'er on the ray from the origin in the management of the eigenvector
that is e'er on the ray from the origin in the management of the eigenvector ![]() . The solution
. The solution ![]() is on the ray in the reverse management. If
is on the ray in the reverse management. If ![]() the motion is outward, while if
the motion is outward, while if ![]() it is inward. As
it is inward. As ![]() (if
(if ![]() ) or
) or ![]() (if
(if ![]() ), these trajectories approach the origin, while as
), these trajectories approach the origin, while as ![]() (if
(if ![]() ) or
) or ![]() (if
(if ![]() ) they go off to
) they go off to ![]() . For complex eigenvalues, on the other paw, the eigenvector is not then useful.
. For complex eigenvalues, on the other paw, the eigenvector is not then useful.
In improver to a classification on the basis of what the curves wait like, we will want to hash out the stability of the origin as an equilibrium point.
Hither, and so, is the nomenclature of the phase portraits of ![]() linear systems.
linear systems.
- If
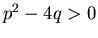 ,
, 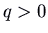 and
and 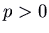 , we take two negative eigenvalues. There are straight-line trajectories corresponding to the eigenvectors. The other trajectories are curves, which come up in to the origin tangent to the ``slow'' eigenvector (respective to the eigenvalue that is closer to 0), and as they go off to
, we take two negative eigenvalues. There are straight-line trajectories corresponding to the eigenvectors. The other trajectories are curves, which come up in to the origin tangent to the ``slow'' eigenvector (respective to the eigenvalue that is closer to 0), and as they go off to 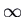 arroyo the direction of the ``fast'' eigenvector.
arroyo the direction of the ``fast'' eigenvector. This example is called a node. Information technology is an attractor.
Here is the picture for the matrix
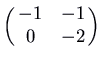 , which has feature polynomial
, which has feature polynomial 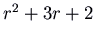 . The eigenvalues are
. The eigenvalues are 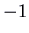 (deadening) and
(deadening) and 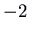 (fast), corresponding to eigenvectors
(fast), corresponding to eigenvectors 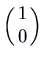 and
and 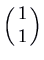 respectively.
respectively. 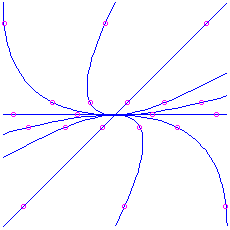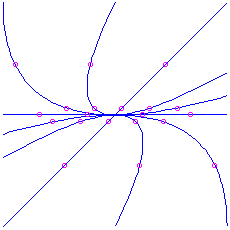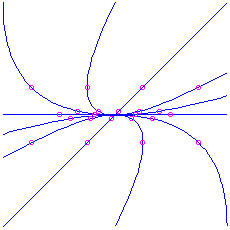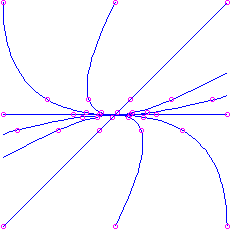
- If
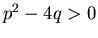 ,
, 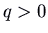 and
and  , we have ii positive eigenvalues. The picture is the aforementioned as in the previous case, except with the arrows reversed (going outward instead of inward). Again the curved trajectories come in to the origin tangent to the ``slow'' eigenvector (corresponding to the eigenvalue that is closer to 0), and as they become off to
, we have ii positive eigenvalues. The picture is the aforementioned as in the previous case, except with the arrows reversed (going outward instead of inward). Again the curved trajectories come in to the origin tangent to the ``slow'' eigenvector (corresponding to the eigenvalue that is closer to 0), and as they become off to  approach the management of the ``fast'' eigenvector. This is also a node, but information technology is unstable. Here is the picture for the matrix
approach the management of the ``fast'' eigenvector. This is also a node, but information technology is unstable. Here is the picture for the matrix 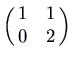 , which has characteristic polynomial
, which has characteristic polynomial 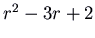 . The eigenvalues are
. The eigenvalues are 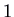 (wearisome) and
(wearisome) and 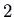 (fast), corresponding to eigenvectors
(fast), corresponding to eigenvectors 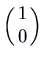 and
and 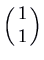 respectively. Note that the picture is exactly the aforementioned every bit what we had for the attractor node, except that the direction of time is reversed (the animation is run backwards).
respectively. Note that the picture is exactly the aforementioned every bit what we had for the attractor node, except that the direction of time is reversed (the animation is run backwards). 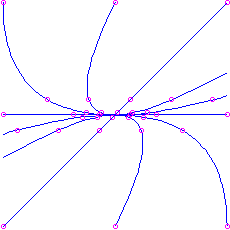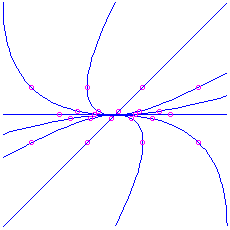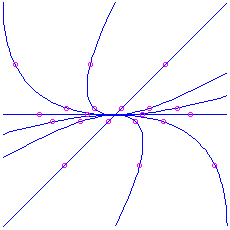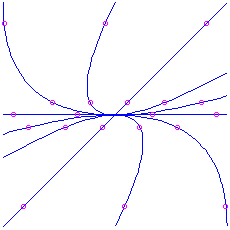
- If
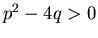 and
and 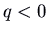 , we have i positive and one negative eigenvalue. Again there are straight-line trajectories respective to the eigenvectors, with the motion outwards for the positive eigenvalue and inwards for the negative eigenvalue. These are the but trajectories that arroyo the origin (in the limit equally
, we have i positive and one negative eigenvalue. Again there are straight-line trajectories respective to the eigenvectors, with the motion outwards for the positive eigenvalue and inwards for the negative eigenvalue. These are the but trajectories that arroyo the origin (in the limit equally 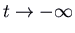 for the positive and
for the positive and 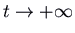 for the negative eigenvalue). The other trajectories are curves that come in from
for the negative eigenvalue). The other trajectories are curves that come in from 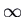 asymptotic to a straight-line trajectory for the negative eigenvalue, and go dorsum out to
asymptotic to a straight-line trajectory for the negative eigenvalue, and go dorsum out to 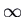 asymptotic to a straight-line trajectory for the positive eigenvalue.
asymptotic to a straight-line trajectory for the positive eigenvalue. This is called a saddle. It is unstable. Notation that if yous first on the straight line in the direction of the negative eigenvalue you do approach the equilibrium point as
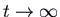 , but if you offset off this line (fifty-fifty very slightly) you end up going off to
, but if you offset off this line (fifty-fifty very slightly) you end up going off to 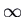 .
. Here is the picture for the matrix
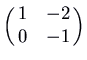 , which has characteristic polynomial
, which has characteristic polynomial 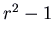 . The eigenvalues are
. The eigenvalues are 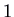 and
and 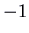 , respective to eigenvectors
, respective to eigenvectors 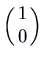 and
and 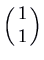 respectively.
respectively. 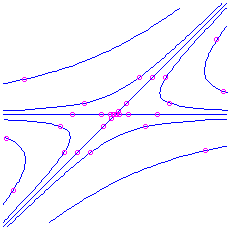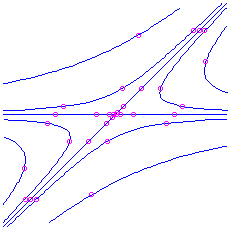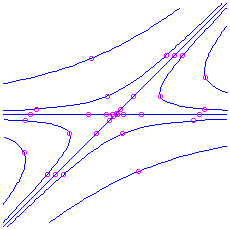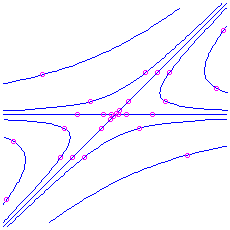
- If
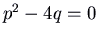 , we have simply one eigenvalue
, we have simply one eigenvalue 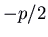 (a double eigenvalue). There are two cases here, depending on whether or non at that place are ii linearly independent eigenvectors for this eigenvalue.
(a double eigenvalue). There are two cases here, depending on whether or non at that place are ii linearly independent eigenvectors for this eigenvalue. - If there are two linearly independent eigenvectors, every nonzero vector is an eigenvector. Therefore we take directly-line trajectories in all directions. The motion is e'er inward if the eigenvalue is negative (which means
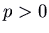 ), or outwards if the eigenvalue is positive (
), or outwards if the eigenvalue is positive (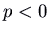 ). This is called a singular node. It is an attractor if
). This is called a singular node. It is an attractor if 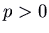 and unstable if
and unstable if  .
. Hither is the picture for the matrix
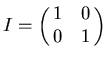 , which has feature polynomial
, which has feature polynomial 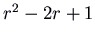 and eigenvalue
and eigenvalue 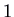 . Information technology is unstable. For the matrix
. Information technology is unstable. For the matrix 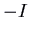 nosotros would have an attractor: the same movie except with time reversed.
nosotros would have an attractor: the same movie except with time reversed. 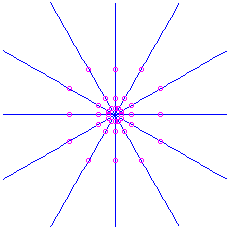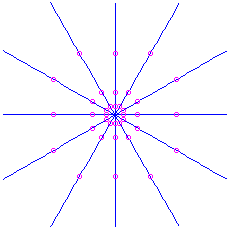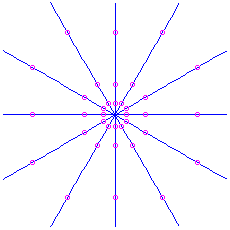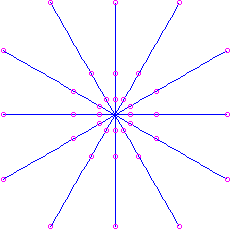
- If at that place is just one linearly independent eigenvector, there is only one straight line. The other trajectories are curves, which come in to the origin tangent to the directly line trajectory and curve around to the opposite direction. Trajectories on reverse sides of the direct line form an ``Southward'' shape. The mode to tell whether it is a forwards South or backwards S is to look at the direction of the velocity vector
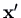 at some bespeak off the straight line.
at some bespeak off the straight line. This is chosen a degenerate node. Again, it is an attractor if
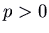 and unstable if
and unstable if 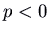 .
. Here is the picture for the matrix
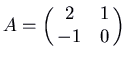 , which has feature polynomial
, which has feature polynomial 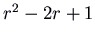 , eigenvalue 1 and eigenvector
, eigenvalue 1 and eigenvector 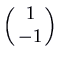 . It is unstable. Notation that the trajectories in a higher place the straight line
. It is unstable. Notation that the trajectories in a higher place the straight line 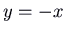 are come up out of the origin heading to the left along that line, and those below the line come up out heading to the right. Thus the South is forwards. To check this, you could calculate the velocity vector at, for example,
are come up out of the origin heading to the left along that line, and those below the line come up out heading to the right. Thus the South is forwards. To check this, you could calculate the velocity vector at, for example, 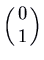 , which is
, which is 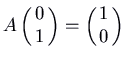 . Since that points to the right, it's easy to see the Southward must exist forwards.
. Since that points to the right, it's easy to see the Southward must exist forwards. 
- If there are two linearly independent eigenvectors, every nonzero vector is an eigenvector. Therefore we take directly-line trajectories in all directions. The motion is e'er inward if the eigenvalue is negative (which means
- If
 and
and 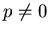 , nosotros have complex eigenvalues
, nosotros have complex eigenvalues 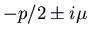 . The solutions are of the class
. The solutions are of the class 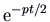 times some combinations of
times some combinations of 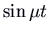 and
and 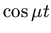 . The picture is a spiral, too known as a focus. It is an attractor if
. The picture is a spiral, too known as a focus. It is an attractor if 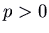 , as the factor
, as the factor 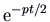 makes all solutions arroyo the origin every bit
makes all solutions arroyo the origin every bit 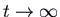 , and unstable if
, and unstable if 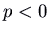 , as in that case the factor
, as in that case the factor 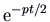 makes all solutions (except the one starting at the equilibrium point itself) go off to
makes all solutions (except the one starting at the equilibrium point itself) go off to 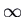 as
as 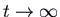 . We tin can summate a velocity vector to check if the motion is clockwise or counterclockwise.
. We tin can summate a velocity vector to check if the motion is clockwise or counterclockwise. Here is the picture for the matrix
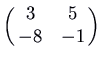 , which has characteristic polynomial
, which has characteristic polynomial 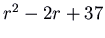 and eigenvalues
and eigenvalues 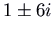 . It is unstable. To check that the motion is clockwise, you could note that the velocity vector at
. It is unstable. To check that the motion is clockwise, you could note that the velocity vector at 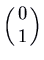 is
is 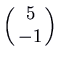 , which is to the right.
, which is to the right. 
- Finally, if
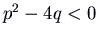 and
and 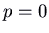 , nosotros have pure imaginary eigenvalues
, nosotros have pure imaginary eigenvalues 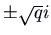 . The solutions involve combinations of
. The solutions involve combinations of 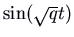 and
and 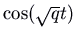 . These are all periodic, with menstruation
. These are all periodic, with menstruation 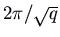 . The trajectories plow out to exist ellipses centred at the origin. The picture is known equally a centre. Since a solution that starts about the origin simply goes around and around the same ellipse, never getting any closer to or farther from the equilibrium than the closest and farthest points on the ellipse, this equilibrium is stable but not an attractor. Again we can summate a velocity vector to run into whether the motion is clockwise or counterclockwise.
. The trajectories plow out to exist ellipses centred at the origin. The picture is known equally a centre. Since a solution that starts about the origin simply goes around and around the same ellipse, never getting any closer to or farther from the equilibrium than the closest and farthest points on the ellipse, this equilibrium is stable but not an attractor. Again we can summate a velocity vector to run into whether the motion is clockwise or counterclockwise. Here is the moving picture for the matrix
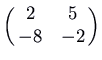 , which has feature polynomial
, which has feature polynomial 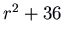 and eigenvalues
and eigenvalues 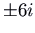 . Once again you tin check that the motion is clockwise by noting that the velocity vector at
. Once again you tin check that the motion is clockwise by noting that the velocity vector at 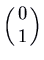 is
is 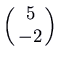 , which is to the right.
, which is to the right. 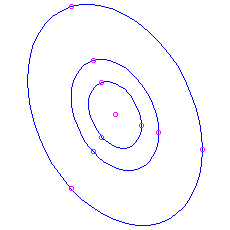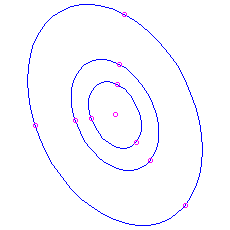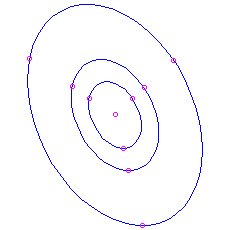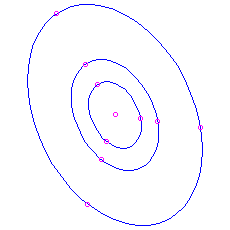
- About this certificate ...
Robert Israel
2002-03-24
colliermagesentrage1994.blogspot.com
Source: https://www.math.ubc.ca/~israel/m215/linphase/linphase.html
0 Response to "How to Draw Phase Plane Trajectory"
Postar um comentário